Cryptanalysis 101

Cryptanalysis is the science and art of attacking cryptosystems. In most cases the term specifically refers to finding flaws in encryption algorithms. The proper design of ciphers cannot be accomplished without having knowledge of the attacks against them. I don't think any other security field requires that the defender be this good at attacking. New cipher designs must be subjected to cryptanalysis by both the author and other researchers before being considered for use. This of course is not always true and many product employ what is called homegrown crypto (attacks that non-cryptographers naively create as an afterthought). Anyway, the ultimate goal of an attack is to recover the key being used to encrypt the target information.

Brute Force vs. "Breaks"

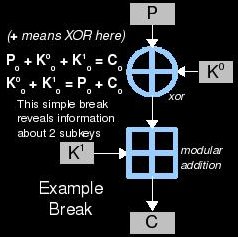
There is one method of key recovery which is always available: brute force. This means trying every possible key and using it to decrypt some collected ciphertext. Eventually you will hit the correct key and you win. Now what does "eventually" mean? Well, the worst-case scenario is that the correct key will be the last one you test. On average, the key will be found at the half-way mark. The number of possible keys is called the keyspace and the amount of information (bits) that is takes to represent a key inside this keyspace is called the key length. Cryptanalysts try to find breaks in the system/cipher. Although this term is a general one (similar to "hack" but specific to crypto), it pretty much means a trick to discover the key with greater probability and/or in less computational work than brute force. This includes identifying key candidates that are more likely than others and also eliminating key candidates that are less likely than others. The less work that needs to be done to recover the key using this trick is one aspect of what makes some breaks more impressive than others.

Classifying Attacks

Now that we have defined "breaking" a cipher in pretty wide terms (i.e: find a problem), it's time to broadly classify some cryptanalytic attacks. One method of categorizing them is by asking "What power/information is needed to perform the attack?" In all of these situations, the same key is expected to be used throughout and the goal to to recover it. Here are a few of the more common types of attacks:

• Black box - In almost every cryptanalytic challenge, it is assumed that the attacker has full knowledge of the inner workings of the algorithm in use and lacks only the key. Black box analysis is the exception. This sort of analysis should not be used to certify the security of an algorithm, but it is sometimes necessary in the real world. Also, just because the algorithm is unknown, that doesn't mean that the situation is also a ciphertext-only one.


• Ciphertext-only - This is a very difficult situation to be in: knowing only some ciphertext. You can imagine an attacker sitting on a network and sniffing an encrypted data stream. In this case, he doesn't know any of the cooresponding plaintext at all, but may have statisical information about it (English language ASCII text for example). Typically the more of this ciphertext that is gathered, the better chance that it will succeed or the less work will need to be done.


• Known-plaintext - This one is a bit more difficult but opens the door to stronger attacks. If we are able to collect some ciphertext and also some of the plaintext that created it (using the cipher and the target key), we can try known-plaintext breaks. The idea here is to compare that plaintext to the resulting ciphertext and learn statistical information about the relationship. This can then be used to narrow the keyspace and predict likely keys. Again, the more plaintext-ciphertext pairs we can gather: the better. A real-world example might be an enemy sending sea condition reports back to HQ. Because we can look at the ocean, it should be pretty easy to guess what they are sending (the plaintext). If we can also intercept the resulting encrypted radio transmissions, a known-plaintext break could be used to recover the key (which may also protect more important information).


• Chosen-plaintext - One of the hardest levels of control an attacker can achieve is chosen-plaintext: being able to make the enemy encrypt whatever we want with the target key and be able to recover the resulting ciphertext. It is also allows more powerful attacks including differential cryptanalysis. This may seem like a very improbable situation, but give it a think. Wartime example: By sending a lot of tanks into battle, we can pretty much guarantee that the enemy will report the situation over encrypted radio (with the word "tank" in the plaintext). Depending on how crafty we are, its almost as if they will send whatever we like after encrypting it with their secret key.

Frequency Analysis

Cryptogram puzzles are solved for enjoyment and the method used against them is usually some form of frequency analysis. This is the act of using known statistical information and patterns about the plaintext to determine it. In cryptograms, each letter of the alphabet is encrypted to another letter. This table of letter-letter translations is what makes up the key. Because the letters are simply converted and nothing is scrambled, the cipher is left open to this sort of analysis; all we need is that ciphertext. If the attacker knows that the language used is English, for example, there are a great many patterns that can be searched for. Classic frequency analysis involves tallying up each letter in the collected ciphertext and comparing the percentages against the English language averages. If the letter "M" is most common then it is resonable to guess that "E"-->"M" in the cipher because E is the most common letter in the English language. These sorts of clues can be bounced off each other to derive the key and the original plaintext. The more collected ciphertext the attacker has, the better this will work. As the amount of information increases, its statistical profile will draw closer and closer to that of English (for example). This sort of thing can also be applied to groups of characters ("TH" is a very common combination in English for example). The example frequency analysis image above was performed on the first three sentences of this paragraph turned into a cryptogram. As you can see, the English language is very predictable with regard to letter frequency and this can exploited in some situations to break ciphers.

Toy Ciphers and Practicing

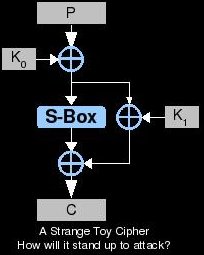
As we learn more about cryptanalysis and read papers about attacks, we'll need a way to actually learn what is read. I like to create toy ciphers to try out attacks or develop new ones. These are encryption algorithms that are invented for the purpose of being broken. You can just string some cipher components together in a way that makes sense for the attack you'd like to try. By starting simple and not just copying whatever cipher is broken in the paper you're reading, you can learn a lot more. Also, more practice can be had by applying techniques against weakened variants of real-world ciphers. I also find it helpful to shrink the block and key sizes down a lot when first trying something new. This allows some results to be worked out by hand with pen/paper and can aid in troubleshooting code. The paper "Self-Study Course in Block Cipher Cryptanalysis" by Bruce Scheneir describes some weakened cipher variants for beginners and makes a good starting point.

Linear and Differential Cryptanalysis

Here I will briefly describe (only an overview) two of the most revolutionary analysis methods for cryptography in recent years. A great deal of new research stems from them and understanding the methods is important. I urge the reader to take their time as they read more into these subjects. Ask yourself questions "why is that?", "what does that mean?", "how can i test that out?". I'm a firm believer that passively reading something is useless compared to actively reading it. Differential cryptanalysis is an attack published by Eli Biham and Adi Shamir in 1990. It was discovered earlier by both IBM (1974) and the NSA (who knows?) but kept secret. It is a chosen-plaintext attack that involves choosing plaintexts in pairs with a particular XOR difference and looking for a corresponding XOR difference in the pairs of ciphertext produced. Linear cryptanalysis was discovered and published by Mitsuru Matsui in 1992 as an attack on FEAL. It is a known-plaintext attack that builds a linear approximation of the cipher (using XOR operations on various bits) and then compares the expression to the collected plaintext to estimate the likely keys.