Block Ciphers

Block Ciphers are cryptographic algorithms that process data in chunks called blocks. Plaintext blocks are combined with a key to produce ciphertext blocks. The datails of this combining is what determines the strength of the cipher. However, these details should not be kept secret. In academic cryptanalysis, it is assumed that the attacker has full knowledge of the algorithms inner-workings and lacks only the key. Thus, ciphers are designed in such a way that all of the security rests on keeping the key secret.

Key Expansion

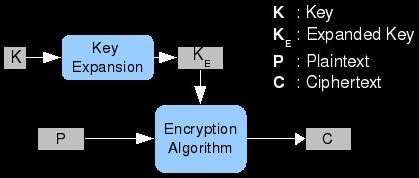
Before we can combine a key with a block of plaintext; we must ensure that their lengths correspond in some meaningful way. For example, the block size and the key length could be identical. This would lead to some easy computation and maximize the effective use of the key bits. Sometimes there is a need for more key material than just the original key; in these cases, the algorithm must employ a key expansion algorithm. We could have a block size of 256 bits but a key length of only 128 bits. The simplest key expansion method is to simply repeat the key until there is enough key material. This is a pretty bad idea though; repetition of the key should be avoided during cipher design. Also, the key expansion algorithm does not need to be reversible; it only provides more key material from which the original key does not need to be recoverable. In this way, key expansion is similar to hashing except that we are expanding rather than compressing.

Substitution-Permutation Networks

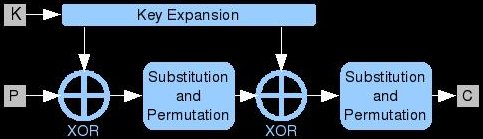
SPNs are a popular way to structure ciphers and are simple enough for us to approach at this point. The plaintext block is processed multiple times during encryption (and decryption). The process that is repeated is called a round function; these rounds are chained together back-to-back to form the full algorithm. Each round takes input data and a subkey, combines them, performs some substitution and permutation, and produces the output. Subkeys are created from the original key by a key expansion algorithm designed for multiple-round ciphers called a key schedule. A popular method of combining a subkey with data is bitwise XOR. In each round, after the key mixing, the data is scrambled further using substitution and permutation functions.

Key Mixing

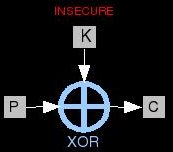
Key Mixing is the element of a cipher in which the data meets the key material. Many times this is one of the simplest portions of the algorithm. It often consists of simply XORing the data with key material of the same length. XOR has some very interesting properties that make it useful in cryptography. If an input is XOR'd with a key to produce an output; this output can then be XOR'd with the same key to produce the input again. In other words: P K = C and C K = P. There is another equation which holds true and is of interest to cryptanalysts: P C = K. What this means is that if a cipher uses only XOR, it is trivially vulnerable to a known-plaintext attack. In other words, if an attacker can capture one block of plaintext and one block of the corresponding ciphertext; he can derive the key. The attacker just needs to XOR the two blocks together; adding more rounds won't help and neither will adding substitution/permutation. However, integrating both of these elements into the cipher properly will remedy this simple attack. This key mixing XOR stage of the cipher is completely linear; the substitution/permutation elements are required to add non-linearity to the algorithm.

Permutation Boxes

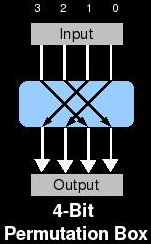
This is an element of ciphers that adds Diffusion to the algorithm. The objective of diffusion is to spread information around in the ciphertext. A group of techniques called frequency analysis take advantage of patterns in the input data (i.e. the English language) to help deduce the plaintext. Ciphers using only substitution are vulnerable to these attacks. The simplest example is the monoalphabetic cipher used in puzzles called cryptograms. These puzzles lack any diffusion at all and are so vulnerable to frequency analysis that they can be solved by hand for fun. P-Boxes can be added to ciphers to introduce diffusion. These are very simple functions that move bit values from one position to another. For example, a P-Box might switch the values of Bit₀ and Bit ₂ during encryption (and the same during decryption).

Substitution Boxes

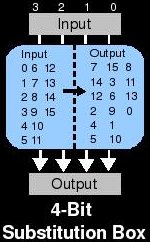
S-Boxes add something called confusion to ciphers that employ them. They obscure differences between the plaintext and the ciphertext. By properly adding confusion to a cryptographic algorithm, we can make it more resistant to differential and linear cryptanalysis. Substitution functions must be reversible in order to allow decryption and by themselves they provide no security. But when combined with diffusion and key mixing over multiple rounds, security can be achieved. The simplest type of S-Box takes input and checks a lookup table to determine the output. In the decryption routine, this lookup table is obviously reversed. The design of substitution boxes is very tricky business and requires a deep understanding of modern cryptanalytic methods. Basically, input patterns into the box should produce patterns in the output with a probability close to that of a random function. Example: if you XOR all of the input bits with each other across all possible inputs, a perfect s-box would produce the same XOR'd value in exactly half of the corresponding outputs.

Feistel Ciphers

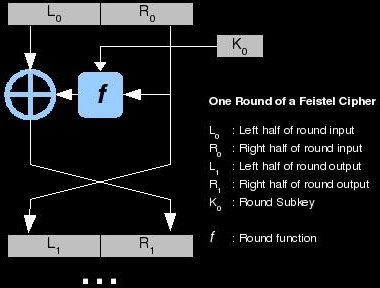
There are a lot of ways that we can structure a block cipher; the first one we explored with the basic SPN. Another structure, which is extremely popular, is a Feistel cipher. What makes Feistel structures so useful is that the round function (the meat of the algorithm) in them can be very similar or even the same in the encryption and decryption functions. This means that deploying a cryptosystem that uses a Feistel-like structure might require half the code than other algorithms. These types of ciphers have also become popular because DES (Data Encryption Standard) uses a Feistel structure. DES is probably the most studied algorithm in history and much research, and therefore ciphers, is based on it. Data comes into the algorithm and is split into two halves: left and right. The right side is combined with a subkey from a key expansion algorithm (key schedule) using the round function. The round function typically involves key mixing, substitution, and permutation. The output of the round function is then XOR'd with the left half; this produces the next round's right half. The next round's left half is simply the current round's right half. This chunk of processing is called a round and each round gets a subkey. Typically, the more rounds in a cipher, the more secure it is. There are a great many research papers out there that deal with Feistel structures and it will benefit the reader to understand them well.