Rakewalking

I don't do much raking these days; it seems like a very luck-driven technique. Its effectiveness in right hands cannot be argued, however. Some locks just seem to fall open when faced with raking. The success that both beginners and experts have experienced with it is evidence enough that it is a valid technique. I wanted to find out what the most effective raking technique is. If you asked around, the responses would likely be vague and hard to put into words. Tension control is a very important element in raking that musn't be ignored, but I'm curious about the use of the rake itself. With the goal in mind of finding the best raking technique, I sat down at the computer and started writing code.

Our Model

In order to find the most efficient raking technique, we must first define what raking is. The term is thrown around by a lot of folks (myself included) as a synonym for "random chaotic movement". Here, we will make it synonymous with an older term: Scrubbing. As the name implies, scrubbing is the act of moving a pick along the bottoms of the pins in a forward-and-back motion under tension. The goal is to randomly set pins until the lock opens. For now, I'm only concerned with outward stroke of the tool. This technique of raking from the back of the lock toward the keyway is a common one and is a good starting point for analyzing these sorts of movements.

Now in order to simulate this action on a computer, I had to hypothesize how this techique opens locks. This model is not perfect, but it seems like a plausible one. We assume that the picker is using perfect tension during the raking. That is, not so much tension that binding pins cannot move but enough to bind them. If the pick encounters a non-binding pin, it move it out of way and continue. If it encounters a binding pin, it will also move it out of the way until it set. Because the tension is perfect, it will not overset the pin as the pick continues moving out of the lock. Instead, the pick will be deflected downward until it clears the set pin. It will continue from this deflected position until the rake is finished. In other words, the picker is not exerting any upward pressure while drawing the rake out of the keyway. The virtual rake is actually a half-diamond that is shaped in such a way that it can lift a pin to its highest bitting without disturbing the other pins.

In order to make this model more clear, I made a little 3d video which can viewed by clicking the thumbnail to the left. This video was not generated by the program I wrote, I just threw it together using Blender. Green pins are set, red are binding, and white are non-binding. Watch it a few times to get feel for the assumptions I'm making.

What is Rakewalking?

If we assume the above model to be correct, then simply raking from the back repeatedly is not very effective. Rakewalking gives much better results and is a very simple concept. Instead of raking from the back, you rake outward from behind a particular pin. So a normal outward rake could also be called "Rakewalk from pin 5" (on a 5 pin lock). By starting your raking action from a pin other than the last one, you can avoid some of the deflection and hopefully improve the success-rate. This is not some revolutionary concept, just a rake that starts from a certain pin and moves toward the picker in a swipe.

The Simulation

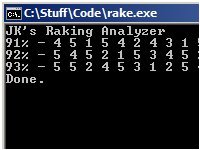
I wrote a little program in C that will test out a bunch of rakewalking combinations to find out the most effective ones. So for instance, it may try out rakewalking from pin 5, then 3, then 5 again, then 2. It does this while retaining tension through the combo/attempt. There is no randomness in the actual process of the rake; only in the test cases. First it selects a rakewalking combo of a certain length, then it generates 10,000 random locks. These virtual locks have random bittings (10 pin lengths) with no MACS and a random binding order. The program tries to open these locks with the random rakewalking combo and records the success rate. After doing all of this 200,000 times, it displays the rakewalking combo with the best sucess-rate. This is the original mode of operation; the new one tries every single rakewalking combo. This give more accurate results and ensures that no diamonds in the rough are missed. The lock bittings are still random, however.


Download

I sloppily converted this test-app into a somewhat user-friendly one. Inside the source, you will find many bad programming habits (including at least one goto statement!) and inefficiency. If someone wants to wade through and omptimze it or otherwise clean it up, they would rock. Download this zip file which includes both the EXE and the source code. Also, I should note that this thing outputs the results to a file in the same directory as the EXE (wherever that my be) called results.txt.






The Results

The results of the app are interesting but have not been tested extensively. If you try these out, feel free to drop me an email about how it went. If it seems like a promising technique, I'd love to know. Also, if it seems like a bunch garbage, I'd love to know that too. This is all theoretical at the moment and real-world results is what matters in the end. To try these out, simply read the combo from left to right and do a pull-out scrub/rake from behind the pin listed. Keep tension and do the next one. The higher the pin number, the deeper it is inside the lock. The success rate (versus 20,000 virtual locks) is also listed for reference. The results below have been updated based on the new non-random data unless otherwise noted.

Best 5x Rakewalking Combos:

Best 10x Rakewalking Combos (random mode):

Best 5x Upward Rakewalking Combos: